5.0 Geometria

Foi a segunda matéria, e diferente de Trigonometria me agradou um pouco mais... um pouco. Aqui estudamos mais as figuras e suas medidas.
5.1 História da Geometria

Significa medir a terra (do grego:  "geo" = terra, "metria" = medir), de acordo com o site somatematica.br. Suas origens são persas, que estudavam os astros. Mas foi na Grécia que "a coisa" se desenvolveu, com Euclides, que aperfeiçoou a Geometria até hoje. Como a professora Aline havia citado, eles usavam a Geometria para medir um trecho em um rio, por exemplo, para ver qual o caminho mais fácil. E também o usava na astrologia para ver os astros e estrelas.



 5.2 Figuras Geométricas
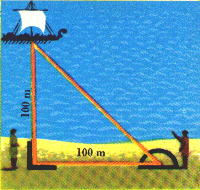
      5.2.1 Triângulo Retângulo - A figura que eu acho mais popular, tem seu catetos e a hipotenusa e forma um ângulo de 90º. Para calcular a área usa-se o Teorema de Pitágoras: h² = x² + y².

Triângulo Retângulo

 Resolvendo o problema com h² = x² + y²:
(√100)²=(√19)² + x²
100=19 + x²
100 - 19 + x²
x = √81
x = 9

   5.2.2 Retângulo - A figura mais fácil de se calcular na minha opinião. Tem-se a base e a altura. Basta calcular base*altura.


Resolvendo o problema com b*h:
5*10 = 50cm²
Logo, a área total do retângulo é 50cm².

   5.2.3 Trapézio - A figura consiste em calcular da seguinte forma. Temos dois lados e uma altura. Fazemos então da seguinte maneira:
AT = (B + b) = h/2 >> onde B é a base Maior e b é a base menor. h é a altura.

Então:

AT = (32 + 25) * 10 / 2

AT = 285

Logo, a área do trapézio é 285cm².

    5.2.4 Quadrado - O quadrado é a figura mais simples de todas. Para a área total é l², onde l são os lados da figura. Para calcular o perímetro, usa-se 4l, onde cada l é os lados.

Para calcular o perímetro, fazemos 4l. Então:

P = 4*20

P = 160cm

Para calcular a área, fazemos l². Então:

A = 20²

A = 400cm²

Então, o perímetro e a área é, respectivamente, 160cm e 400cm²;

    5.2.5 Triângulo Isósceles  - Para calcular o triângulo Isósceles, cortamos primeiro a metade do triângulo e ficará dois triângulos retângulos. Assim como cortamos o Triângulo em duas partes, obtivemos dois triângulos retângulos, que podem formar um retângulo.

Triângulo Isósceles completo

Triângulo Isósceles cortado. Dá forma de um Triângulo Retângulo.

Após cortar e dar a forma de um triângulo retângulo, calculamos com Pitágoras:
h² = x² + y²
20² = 5²+ y²
400 = 25 + y²
400 - 25 = y²
375 = y²
y = √375
y = 19,36


Agora, basta multiplicar por 2  para calcular toda a área to triângulo:
19,36 * 2
ATI = 38,72


Logo, a área total é 38,72cm².

Ajuda do Gabriel Bauer nessa.


  5.3 Inscrito e Circunscrito
       5.3.1 Inscrito - O círculo fica dentro de um quadrado, retângulo ou qualquer outra figura:

Um círculo Inscrito em um Quadrado

  
    5.3.2 Circunscrito - O círculo fica fora de um triângulo, quadrado ou qualquer outra figura:

Um círculo Circunscrito em um Triângulo Retângulo

Fontes: http://www.somatematica.com.br/geometria.php