4.0 Trigonometria

Creio que sinceridade é tudo! Se for, eu resumo aqui: Não gostei nem um pouco dessa matéria, ou pelo menos da forma que a vi! Achei-a confusa e complexa demais. Ok, vamos ver um pouco dos conceitos e história da trigonometria:

4.1 História da Trigonometria

O Papiro Rhind

O site ecalculo.if.usp.br narra que a origem da trigonometria é incerta. Mas pode ter começado devido a problemas na Astronomia, Agrimensura e Navegações. Provavelmente foi criada por egípcios e/ou babilônios por volta do século IV ou V a.C. Sua primeiras aplicações estão escritas no Papiro Rhind e em tábuas babilônicas chamada de Plimpton 322.

Trigonometria significa do grego trigōnon "triângulo" + metron "medida" de acordo com o Wikipédia, onde obviamente estudamos ângulos e suas medidas.

Veja mais sobre a história da Trigonometria aqui.

4.2 As características para calcular um triângulo retângulo:

      4.2.1 Triângulo Retângulo - O tipo de triângulo mais famoso de todos. Possui um ângulo reto e no seu oposto se encontra a hipotenusa. Os outros ângulos são os catetos, oposto no lado inverso do ângulo e adjacente na "mesma linha" do ângulo. Sempre terá um ângulo de 90º.

O Triângulo Retângulo.

 Aqui é possível calcular através do teorema de pitágoras, se dado dois valores (hipotenusa x um dos catetos/ cateto x cateto). Exemplo:

Aqui basta usar a fórmula de pitágoras (h²=x²+y², onde h=hipotenusa e x,y=catetos):

8²=10²+x²

64=100+

x²=100-64

x=√36

x=6, onde x será 6 m/cm/dm.

4.3 A circuferência:

      4.3.1 O que é? - É um círculo (capaz!) onde seu arco completo dá 360º. Do seu centro até o lado tem uma medida x e terá sempre, caso haja uma trajetória, um ângulo e nesta trajetória um radiano.

Circuferência e suas características.

    4.3.2 Os quadrantes - Os quadrantes são nomeados assim para identificar se x e y serão negativos, positivos. Também serve para identificar que ângulo é ali.

A imagem mostra os eixos x e y e sua classificação nos quadrantes.

 4.4 Funções na Circuferência:

       4.4.1 O que é? -  Geralmente quando fizemos um trajetos de dois pontos numa circuferência (A e B), teremos um ângulo do ponto central até eles. Deste ponto até eles terá uma distância e provavelmente duas figuras. Veja a imagem abaixo:

Seja AB, a trajetória. XB são o raio, y e X são as projeções do ponto B para os eixos X e Y.

O seno deste exemplo será AB (ou o ângulo x), então: sen x =xY → xY é a ordenada do pontoB.

     4.4.2  Calcular senos de ângulos - Para calcular o seno de um ângulo é bem simples. Devemos pegar o ângulo que nós é informado e dividir por 360º (é o valor de uma volta completa). Se senoº > 360º então o resultado será voltas + xº restantes. Se senoº < 360 então o resultado não será uma volta completa. Se senoº for ≥ 360º então será uma volta completa. Exemplos:

1) seno 800º

     800º/360º = 2,22, ou seja, aproximadamente 2 voltas e 22º (sobra no primeiro quadrante).

2)seno 360º

     360º/360º = 1, ou seja, uma volta inteira e completa.

3) seno 50º 

     50º/360º = 0,13, ou seja, aproximadamente 0,13º, ou 13º.

   4.4.3 Descobrindo seno, cosseno e tangente de um triângulo retângulo - São através de maneiras simples. Usa-se as seguintes "fórmulas":

Seno = cateto oposto                hipotenusa

Cosseno = cateto adjacente                         hipotenusa

Tangente =    cateto oposto                       Cateto adjacente

 Observe o exemplo abaixo para se encontrar o cosseno:

 Veja que o cosseno é cateto adjcante/hipotenusa. Então:

   cos = 10/5;

    logo, cos = 2

 Agora observe com o seno:

Veja que o seno é cateto oposto/hipotenusa. Então:

sen = 50/5;

logo, cos = 10

E por último, a tangente:

Veja que a tangente é cateto oposto/adjacente. Então:

tag =  √81/√25

tag = 9/5

logo, tag = 1,8

   4.4.4 Ângulos definidos - Para facilitar, há certo ângulos definidos que também podem ser calculados. Os 3 principai são o de 30, 45º, e 60º. Veja a tabela abaixo:

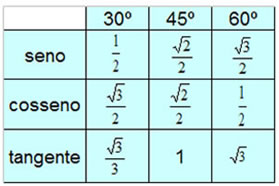Retirado de: http://www.brasilescola.com/matematica/seno-cosseno-tangente-angulos.htm

  Observe então a tabela maior, que abrange quase todos os 100 principais ângulos, tanto para seno, cosseno e tangente:

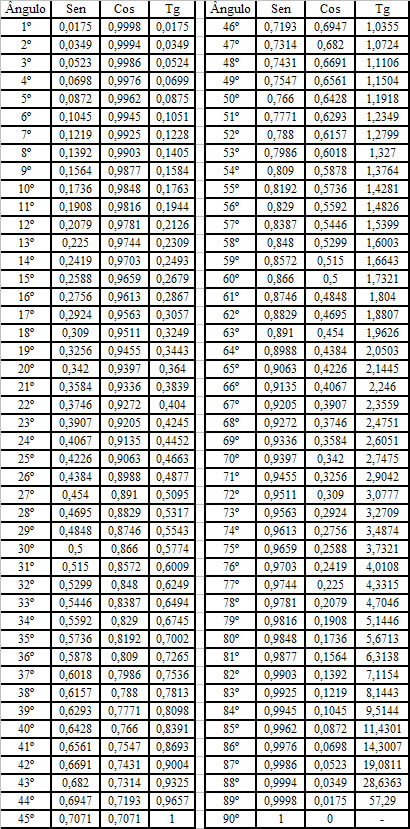Retirado de: http://www.brasilescola.com/matematica/seno-cosseno-tangente-angulos.htm

  Clique aqui para saber mais sobre seno, cosseno e tangente.

    4.4.5 Observações Importantes - Antes de encerrar, gostaria de esclarecer algumas coisas, afinal não descrevi tudo:

* Um π/rad equivale a 180º;

* Uma volta inteira equivale a 2π/rad, pois 1π /rad = 180º;

Fontes e imagens: http://ecalculo.if.usp.br/historia/historia_trigonometria.htm

                              http://pessoal.sercomtel.com.br/matematica/trigonom/trigon1/mod114.htm

                             http://pt.wikipedia.org/wiki/Tri%C3%A2ngulo
Livro Matemática Completa - Ano 2002. GIOVANNI J.R., BONJORNO J.R., JR. GIOVANNI J.R. 
http://pt.wikipedia.org/wiki/Fun%C3%A7%C3%A3o_trigonom%C3%A9trica
http://www.brasilescola.com/matematica/seno-cosseno-tangente-angulos.htm

                           


 OBS.:Provavelmente se pesquisar, verá que na maioria das vezes eu vou ao primeiro site e o coloco como referência. Faço isso devido ao que o Google coloca em primeiro lugar os sites mais acessados, dando referência de confiança e um número elevado de leitores.